TensorFlow 2.0 (九) - 强化学习 70行代码实战 Policy Gradient
源代码/数据集已上传到
Github - tensorflow-tutorial-samples

这篇文章是 TensorFlow 2.0 Tutorial 入门教程的第九篇文章。
实战策略梯度算法(Policy Gradient),代码70行
CartPole 简介
在之前的文章中,我们使用过纯监督学习的算法,强化学习算法中的Q学习(Q-Learning)和深度Q网络(Deep Q-learning Network, DQN),这一篇文章,我们选择策略梯度算法(Policy Gradient),来玩一玩 CartPole。
先回顾一下CartPole-v0的几个重要概念。
| 概念 |
解释 |
示例 |
| State |
状态,[车位置, 车速度, 杆角度, 杆速度] |
0.02, 0.95, -0.07, -1.53 |
| Action |
动作(0向左/1向右) |
1 |
| Reward |
奖励(每走一步得1分) |
1.0 |
我们在 TensorFlow 2.0 (八) - 强化学习 DQN 玩转 gym Mountain Car这篇文章中,介绍了基于价值(value-based)的强化学习算法 DQN,在 DQN 中,神经网络的输入是状态,输出是每一个动作的价值。每一次从所有可行的动作中选择Q值最大的执行。我们使用了一个公式来不断地计算期望的Q值,训练神经网络。
那有没有可能,直接输出动作呢?这就是我们今天要介绍的基于策略(policy-based)的策略梯度算法(Policy Gradient)。
本文不涉及数学推导,仅介绍如何高效实现。如对该算法该兴趣,推荐 Medium 上有3.8k点赞的一篇文章An introduction to Policy Gradients。
搭建神经网络
Policy Gradient 网络的输入也是状态(State),那输出呢?每个动作的概率。例如 [0.7, 0.3] ,这意味着有70%的几率会选择动作0,30%的几率选择动作1。相对于 Policy Gradient,DQN 的动作更确定,因为 DQN 每次总是选择Q值最大的动作,而Policy Gradient 按照概率选择,会产生更多的不确定性。
废话不多说,神经网络先搭起来吧~
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
|
import matplotlib.pyplot as plt
import gym
import numpy as np
from tensorflow.keras import models, layers, optimizers
env = gym.make('CartPole-v0')
STATE_DIM, ACTION_DIM = 4, 2
model = models.Sequential([
layers.Dense(100, input_dim=STATE_DIM, activation='relu'),
layers.Dropout(0.1),
layers.Dense(ACTION_DIM, activation="softmax")
])
model.compile(loss='mean_squared_error',
optimizer=optimizers.Adam(0.001))
|
我们的神经网络很简单,输入层为4,输出层为2,隐藏层为100。不过这次代码多了一个Dropout,Dropout(0.1) 的含义是,随机忘记10%的权重。学习初期,一开始的数据质量不高,随着学习的进行,质量才逐步高了起来,一开始容易陷入局部最优和过拟合,使用 Dropout 可以有效避免。
如何选择动作呢?前文已经介绍,按照概率。
1
2
3
4
5
6
|
def choose_action(s):
"""预测动作"""
prob = model.predict(np.array([s]))[0]
return np.random.choice(len(prob), p=prob)
|
优化策略
接下来是最大的问题,如何优化策略呢?
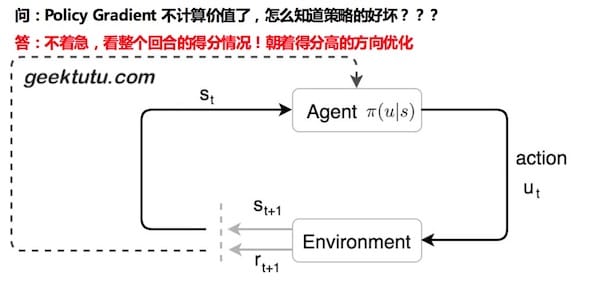
1) 衰减的累加期望
我们先想象一下,假如你在玩坦克大战,你的每一步都会对后面的局势产生巨大的影响。比如,敌方攻打你的老巢,你是选择先消灭敌方呢,还是选择坐视不理?很可能一步就决定了结局。因此,需要从整个回合的角度看待这个问题。先引入一个概念 带衰减reward的累加期望 。
discount_reward[i] = reward[i] + gamma * discount_reward[i+1]
某一步的累加期望等于下一步的累加期望乘衰减系数gamma,加上reward。
手工算一算。
1
2
3
4
| 最后一步:1
倒数第二步:1 + 0.95 * 1 = 1.95
倒数第三步:1 + 0.95 * 1.95 = 2.8525
倒数第四步:1 + 0.95 * 2.8525 = 3.709875
|
假设某个回合只得了10分,那么这个回合的每一步的累加期望都不会高。假设得到了满分200分,那么回合中的大部分步骤的累加期望很会很高,越是前面的步骤,累加期望越高。
代码实现就很简单了,唯一的不同是最后加了中心化和标准化的处理。这样处理的目的是希望得到相同尺度的数据,避免因为数值相差过大而导致网络无法收敛。
1
2
3
4
5
6
7
8
9
10
|
def discount_rewards(rewards, gamma=0.95):
"""计算衰减reward的累加期望,并中心化和标准化处理"""
prior = 0
out = np.zeros_like(rewards)
for i in reversed(range(len(rewards))):
prior = prior * gamma + rewards[i]
out[i] = prior
return out / np.std(out - np.mean(out))
|
2) 给loss加权重
一个动作的累加期望很高,自然希望该动作出现的概率变大,这就是学习的目的。一般,我们通过构造**标签(y_true/label),来训练神经网络。就如在TensorFlow 2.0 (六) - 监督学习玩转 OpenAI gym game这篇文章中做的一样。当然,我们还可以通过改变损失函数(loss function)**达到目的。对于累加期望大的动作,可以放大loss的值,而对于累加期望小的动作,那么就减小loss的值。这样呢?神经网络就能快速朝着累加期望大的方向优化了。最简单的方法,给loss加一个权重。
所以我们的最终的损失函数就变成了:
loss = discount_reward * loss
这里的discount_reward可以理解为策略梯度算法(Policy Gradient)中的梯度(Gradient)。如果对梯度不熟悉,可以看第一篇文章TensorFlow入门(一) - mnist手写数字识别(网络搭建)。
在TensorFlow 1.x的版本中,搭建一个自定义loss的网络很复杂,而使用TensorFlow 2.0,借助Keras,我们可以写出非常简洁的代码。
1
2
3
4
5
6
7
8
9
10
11
12
13
|
def train(records):
s_batch = np.array([record[0] for record in records])
a_batch = np.array([[1 if record[1] == i else 0 for i in range(ACTION_DIM)]
for record in records])
prob_batch = model.predict(s_batch) * a_batch
r_batch = discount_rewards([record[2] for record in records])
model.fit(s_batch, prob_batch, sample_weight=r_batch, verbose=0)
|
设置参数sample_weight,即可给loss设权重。
训练过程与结果
接下来,把 OpenAI gym 的代码融入进来吧。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
|
episodes = 2000
score_list = []
for i in range(episodes):
s = env.reset()
score = 0
replay_records = []
while True:
a = choose_action(s)
next_s, r, done, _ = env.step(a)
replay_records.append((s, a, r))
score += r
s = next_s
if done:
train(replay_records)
score_list.append(score)
print('episode:', i, 'score:', score, 'max:', max(score_list))
break
if np.mean(score_list[-10:]) > 195:
model.save('CartPole-v0-pg.h5')
break
env.close()
|
运行一下试一试吧。
1
2
3
4
5
6
7
8
9
10
| $ python policy_gradient.py
episode: 0 score: 13.0 max: 13.0
episode: 1 score: 35.0 max: 35.0
episode: 2 score: 18.0 max: 35.0
...
episode: 793 score: 200.0 max: 200.0
episode: 794 score: 200.0 max: 200.0
episode: 795 score: 164.0 max: 200.0
episode: 796 score: 200.0 max: 200.0
model saved
|
画一张图,感受下学习的过程,这一次稍微多了3行多项式拟合的代码,能够更好地展现整个分数变化的趋势。
1
2
3
4
5
6
7
|
plt.plot(score_list)
x = np.array(range(len(score_list)))
smooth_func = np.poly1d(np.polyfit(x, score_list, 3))
plt.plot(x, smooth_func(x), label='Mean', linestyle='--')
plt.show()
|
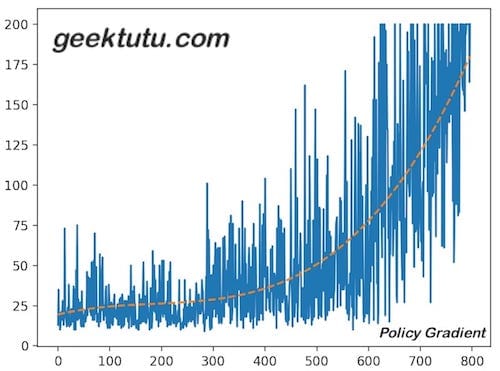 。
。
测试
按照惯例,测试下效果。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
|
import time
import numpy as np
import gym
from tensorflow.keras import models
saved_model = models.load_model('CartPole-v0-pg.h5')
env = gym.make("CartPole-v0")
for i in range(5):
s = env.reset()
score = 0
while True:
time.sleep(0.01)
env.render()
prob = saved_model.predict(np.array([s]))[0]
a = np.random.choice(len(prob), p=prob)
s, r, done, _ = env.step(a)
score += r
if done:
print('using policy gradient, score: ', score)
break
env.close()
|
1
2
3
4
5
6
| python test_policy_gradient.py
using policy gradient, score: 200.0
using policy gradient, score: 200.0
using policy gradient, score: 200.0
using policy gradient, score: 200.0
using policy gradient, score: 200.0
|

如何优化
教程中,每个回合不管多少条训练数据,直接训练,而没有固定大小的batch,不利于训练。有时间可以尝试,设置一个大小为2000的队列,存储历史的训练数据,每次固定取32/64条训练集,对比下两者的效果。
代码已上传至 Github - CartPole-v0-policy-gradient
附 推荐
上一篇 « 博客折腾记(五) - 友链这件事,没那么简单
下一篇 » TensorFlow 2 / 2.0 中文文档


 。
。



